Karmaşık Yükler Altında Yorulma Ömrü Nasıl Hesaplanır?

by Osman Bahadır Özden · Published Nisan 20, 2023 · Updated Nisan 20, 2023

Gerçek yapılara uygulanan çevrimsel yükün değişkenliği ve karmaşıklığı nedeniyle yapıların yorulma ömrünü tahmin etmek genellikle zordur. Malzemelerin SN (Wöhler) verileri sabit genlikli yüklemelerden elde edilir. Bu yazıda gerçek dünyadaki karmaşık yükleri temsil eden bir yükleme altında yapının yorulma ömrünün nasıl hesaplandığı anlatılacaktır.
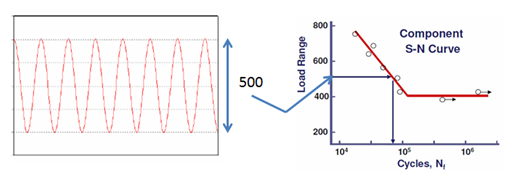
En temel yorulma yükü, Şekil 1’in solunda sinüs dalgası ile temsil edilen sabit genlikli, tam tersine dönen yüklemedir. Tamamen tersine çevrilen yüklemede, minimum yükün maksimum yüke oranı (R oranı) -1’e eşittir. Çoğu yorulma testi için bu yükleme şekli kullanıldığından yorulma ömrünün belirlenmesi için Şekil 1’in sağında gösterilen SN eğrisi kullanılabilir.

Yorulma yüklemesi daha karmaşık ise, ilk önce yükleme çevriminin içeriği çıkarılmalıdır. Yükleme, Şekil 2’de solda gösterildiği gibi sabit genlikli bloklardan oluşuyorsa, bu işlem nispeten basit olabilir. Bu durumda, her bir sabit genlik yüklemesinin genliği ve çevrim sayısı çıkarılarak Şekil 2’nin sağında gösterildiği gibi ayrı ayrı değerlendirilebilir.

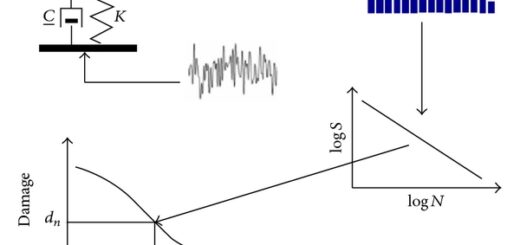
Bir yükleme bloğunun hasara uğradığı döngü sayısı bulunduğunda, kümülatif hasarı tahmin etmek için doğrusal bir hasar kuralı kullanılır. Bu amaç için kullanılan Palmgren-Miner Kuralı aşağıda gösterilmektedir. Burada n her bloktaki döngü sayısıdır ve N_f ise bu yükleme genliği için hasarın oluştuğu çevrim sayısıdır:

$\sum \frac{n_{i}}{N_{fi}}=\frac{n_{1}}{N_{f1}}+\frac{n_{2}}{N_{f2}}+...=1$

Bu hasar kuralının, yükün uygulanma sırasına veya yüklerin birbirine olabilecek herhangi bir etkisine bakılmaksızın, her yükü ayrı ayrı ele aldığına dikkat edilmelidir. Bu hasar kuralı çok basit olsa da, çoklu çevrimsel yüklemenin yorulmaya etkisini incelemek için standart yaklaşım olmaya devam etmektedir.

Gerçek yükleme geçmişi Şekil 3’te olduğu gibi daha karmaşıksa, çevrimsel bilgilerin çıkarılması zor olabilir.

Rainflow Çevrim Sayma Metodu

Yağmur akışı (Rainflow) sayımı olarak bilinen bir teknik, karmaşık yüklemenin çevrimsel verilerini çıkarmak için yaygın olarak kullanılır. Bu tekniğin uygulanması aşağıdaki gibi beş aşamada gerçekleştirilir:

Gerilmelerin tepe ve vadilerini belirleyin ve mutlak maksimumdan başlayarak yeniden sıralayın (Şekil 4).
En derin vadiden başlayarak içerisine su doldurmuş gibi görselleştirin (Şekil 5).
İçerideki suyu boşalttığınızda ortaya çıkan toplam gerilme genliğini, ortalama gerilmeyi ve bu çevrimlerin sayısını ölçün (Şekil 5).
Bir sonraki en düşük vadiyi boşaltarak devam edin ve tüm vadiler boşalana kadar işlemi tekrarlayın (Şekil 6).
Yorulma ömrünü elde etmek için hasar kuralını kullanın.

Tüm çevrimler elde edildiğinde Palmgren-Miner Kuralı uygulanır. Bu kuralda ortalama gerilmenin etkisi göz ardı edilmektedir:

$\sum \frac{n_{i}}{N_{fi}}=\frac{1}{N_{f450}}+\frac{2}{N_{f150}}+\frac{1}{N_{f50}}+...=1$

n değeri, elde edilen çevrimlerin sayısı ile değiştirilir. N_f450, 450 genlikli bir gerilme için SN verisinden elde edilen çevrim sayısını temsil eder.

Yağmur akışı yöntemi otomatikleştirilerek karmaşık yükleme içeriği daha verimli ve kolay bir şekilde çıkarılabilir. Örneğin, nCode DesignLife gibi yorulma yazılımları, çevrimsel verinin otomatik olarak çıkarılması için yağmur akışı yöntemini kullanır. Buna ek olarak, DesignLife, hasar oluşacak çevrimlerin sayısını belirlemek için Palmgrem-Miner Hasar Kuralı hesaplamasını otomatik olarak yapar.

Yorulma ömründeki en büyük rolü gerilme genliğinin oynadığı bilinmektedir. Ancak ortalama gerilmenin de yorulma ömrüne etkisi olabilir. Ortalama gerilmenin etkileri genellikle kaynaklı bölgelerin yorulma incelemesinde göz ardı edilir, ancak diğer durumlarda göz ardı edilemez.

Kaynak: https://www.serdarkorkut.com/2018/09/29/karmasik-yukler-altinda-yorulma-omru-nasil-hesaplanir/