Rastgele Titreşim Analizleri

Rastgele titreşim analizinde, yükleme ve cevabın doğada istatistiki olarak bulunduğu ve sıfır-ortalama normal (Gaussian) dağılımla temsil edilebileceği varsayılmaktadır. Bu dağılımı, belli bir yük seviyesinin veya cevabın ortalamadan belirli bir standart sapma içine düşme olasılığı perspektifinden görmek bazen uygun olabilir. Genellikle, 1σ, 2σ ve 3σ (standart sapma) seviyeleri dikkate alınır. Örnek olarak, rastgele bir x(t) Gauss yüklemesi göz önüne alındığında, x(t)’nin ±1σ arasında olma olasılığı %68,3’tür (örneğin, zaman içindeki yüklemenin çoğunluğunun nominal seviyelerde gerçekleştiği, tepe noktalarının daha az sıklıkla meydana geldiği kabul edilir), ±2σ arasında kalma olasılığı %95,4 ve ±3σ için yukarıdaki Şekil 1’de gösterildiği gibi %99,7’dir.

Rainflow çevrim sayma metodunu kullanan zaman alanı yöntemleri de rastgele titreşimlerde uygulanabilir. Bununla birlikte sayısal hesaplama açısından önemli avantajları nedeniyle genellikle frekans alanındaki analizler tercih edilir. Yıllar boyunca geliştirilmiş rasgele bir titreşim yüklemesine dayanarak hasarı hesaplayan birçok frekans tabanlı yöntem vardır. Bu farklı yöntemler, sonlu elemanlar analizlerinde tipik olarak kullanılan 1σ değerine dayanarak yorulma ömrünü hesaplayan çeşitli teknikler kullanır. Örneğin, bir FEM analizinde hesaplanan S_max = 5 ksi maksimum gerilme değeri, S_max‘ın 5 ksi veya daha az olması olasılığını %68,3 (1σ) olarak belirtir. Bu nedenle, yorulma ömrünü hesaplamak için bir yöntem seçilmeli ve istatistiksel değişkenliği hesaba katmak için (hasara uğramama oranı olarak %68,3 kabul edilebilir değilse) bu sonuçlara uygulanmalıdır. Tasarım için kullanılabilecek en basit yaklaşımlardan biri, ±3σ’nın Goodman diyagramına göre sonsuz ömre denk geldiğini varsaymaktır (S_max‘ın 3 x 5 ksi = 15 ksi veya daha az olması olasılığı %99,7’dir (3σ)). Bu yaklaşım çoğu zaman çok konservatif olabilir, bu durumda daha karmaşık yöntemler mevcuttur.

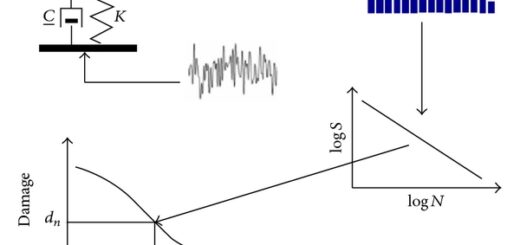
Günümüzde kullanılan tüm yaygın yöntemler, gerçekleşen yorulma hasarının uygulanan gerilme düzeyiyle orantılı olduğunu ve hasarın gerilmelerin uygulanma sırasından bağımsız olduğunu iddia eden Palmgren-Miner hipotezine dayanmaktadır.

Bu teknik kullanılarak yorulma performansı, hesaplanan kümülatif hasar oranı ile belirtilen kümülatif hasar indeksinin karşılaştırılması yoluyla değerlendirilir.

Steinberg 3-bant hasar hesaplama yöntemi basitliği nedeniyle sıkça kullanılmaktadır (Referans 1). Belirli bir bölgedeki gerilme genliği cevabının aşağıdaki üç aralığa bölünmüş bir Gauss dağılımına sahip olduğunu varsayarak, kümülatif yorulma hasarını hesaplamak için Miner Kuralı yaklaşımını kullanır:

• 1σ’da zamanın %68,3’ü
• 2σ’da zamanın %27,1’i
• 3σ’da zamanın %4,3’ü

Bu aralıkların her birinde, hasar oluşması için gerekli çevrimlerin sayısı (N₁, N₂ ve N₃) malzemenin S-N eğrisinden belirlenebilir. Daha sonra, toplam uygulanan çevrim sayısı “n” biliniyorsa, kümülatif yorulma hasarı indeksi R_n‘yi belirlemek için aşağıdaki denklemde gösterildiği gibi Steinberg 3-bant yöntemi kullanılabilir.

 olduğunda hasar oluşur.

Malzeme ömrü tamamlandığında R_n‘nin değeri 1’e eşit olacaktır. Ancak, bu yöntemin belirsizlikleri nedeniyle, hasar endeksi C’ye emniyet faktörleri dahil edilmiştir. Kullanılacak C’nin değeri endüstri ve uygulama standartlarına göre seçilir. Örneğin, elektronikler için test verilerine dayanarak 1 değeri çok yüksek olabilir ve bu değer 0,7 veya 0,3’e düşürülebilir.

Yukarıda anlatılan metodu kullanmak için gereken veriler aşağıdaki gibidir:

1. RMS (1σ) gerilmesi. Bu değer doğrudan sonlu elemanlar analizinden elde edilir. 2σ ve 3σ değerlerini hesaplamak için kullanılır (yani 1σ = 5ksi, 2σ = 10ksi ve 3σ = 15ksi)
2. Malzemenin S-N eğrisi. Bu eğriyi kullanırken göz önünde bulundurulması gerekenler şunlardır:
   1. Eğri, gerilme genliği (maksimum gerilme değil) formunda olmalıdır.
   2. Sıfır-ortalama durağan rastgele işlem için, uygulanan gerilmenin, tamamen tersinir bir gerilme döngüsüne karşılık gelen hem pozitif hem de negatif tepelerden oluştuğu varsayılabilir. S-N eğrisi daha sonra R = -1 oranı için göz önüne alınmalıdır.
   3. S-N eğrisi, malzeme ömründeki herhangi bir ani azalmayı hesaba katmalıdır; eğrinin -3σ seviyesine ayarlanması, yüzey işlemleri vb.
3. Bileşenin zaman içinde maruz kaldığı çevrim sayısı (n). Bu değer aşağıdaki teknik ile hesaplanabilir:
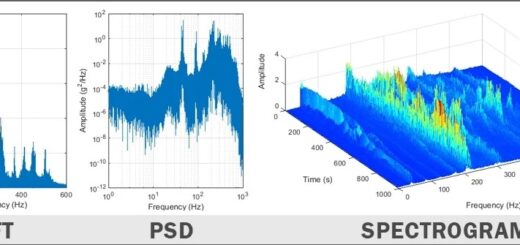
   1. Öncelikle, modeldeki söz konusu konum için istatistiksel ortalama frekansın (zaman başına çevrim frekansı) ne olduğunun belirlenmesi gerekir. FEA yorulma değerlendirmesi frekans alanında yapıldığından, bu değeri hız çözümünü yer değiştirme çözümüne bölerek hesaplayabiliriz (belirli bir gerilme miktarı için ve sonucu birim zaman başına çevrim frekansına çeviririz, örneğin f = ω / 2π). Bu, işlemin birim zaman başına pozitif sıfır geçiş sayısını temsil eder ve dar bantlı durağan bir işlem için, her pozitif sıfır geçişi bir titreşim çevrimini ifade eder.
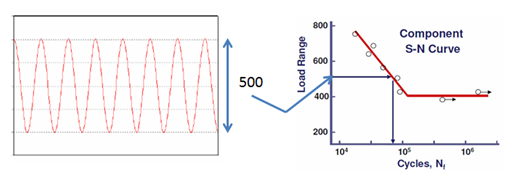
   2. İstatistiksel ortalama frekans hesaplandıktan sonra (örneğimiz için 500 Hz olsun) istatistiksel ortalama çevrim sayısını hesaplamak için bu değeri giriş sinyalinin süresiyle çarpabiliriz. Bu komponent bir titreşim masası üzerinde 2 saatlik bir teste maruz kalırsa, ilgilendiğimiz konum için döngü sayısı 500 Hz x 7200 sn [2 saat] = 3,6 e6 çevrim olacaktır.

Şimdi Steinberg 3-bant yöntemine dayanarak yorulma hasarı R_n‘yi hesaplamak için gereken tüm bilgilere sahibiz. Önceki 1σ gerilmemizi kullanarak, hasar için gerekli çevrim sayısı için Şekil 2’de görülen S-N eğrisini kullanarak N₁ = 2,5 e8 çevrim değerini bulabilir ve aynı işlemi N₂ ve N₃ için tekrarlayabiliriz.

Kaynak: https://www.serdarkorkut.com/2019/06/07/rastgele-titresim-ortaminda-yorulma-hesabi/